A contrivance claimed to be self-balancing
Explaining a popular viral video with a bottle magically hanging from the edge of a table.
While we write this post in June 2020, during COVID times, there is a video that is widely circulated on social media, showing a bottle of water magically defying gravity by hanging from a cantilever without counterweight. This is the video:
Let us try to explain this phenomenon, in an engineering sense.
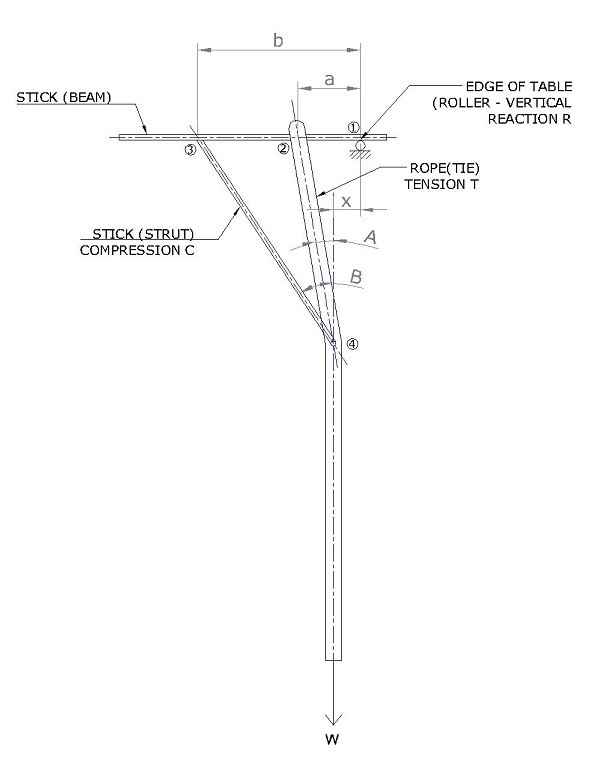
As there is no other external support, Reaction R = W
Equilibrium of forces in beam 1-2-3: C. Cos (B) – T. Cos (A) = W
Resolving forces at Joint 3: Tension in the beam (2 to 3) = C. Sin(B)
Resolving forces at Joint 2: Tension in the beam (2 to 3) = T. Sin(A)
- Sin(B) = T. Sin(A)
Note: if A = 0, then C = 0. That is, the rope is always kinked, it cannot be vertical when strutted.
Equilibrium of Moment about Point 1: Cb. Cos(B) = Ta. Cos(A)
Tb. Sin(A). Tan(B) = Ta. Cos(A)
a/b = Tan(A)/Tan(B)
But, Tan(A)/Tan(B) = (a-x)/(b-x). Either x = 0 or a = b
Thus, x = 0 is true because a = b is a trivial solution which is true only for W = 0
In other words, the strut should tuck the weight W under the table so that centre of mass is directly below the edge of the table.
- Sin(A) Cos(B) – T. Cos(A) Sin (B) = W Sin(B)
T = W Sin(B) / Sin (B-A)
C = W Sin(A) / Sin (B-A)
Interestingly, tie beam 3-2 and strut 3-4 can act as a cantilever system to carry additional loads by pushing the weight, further below the table.
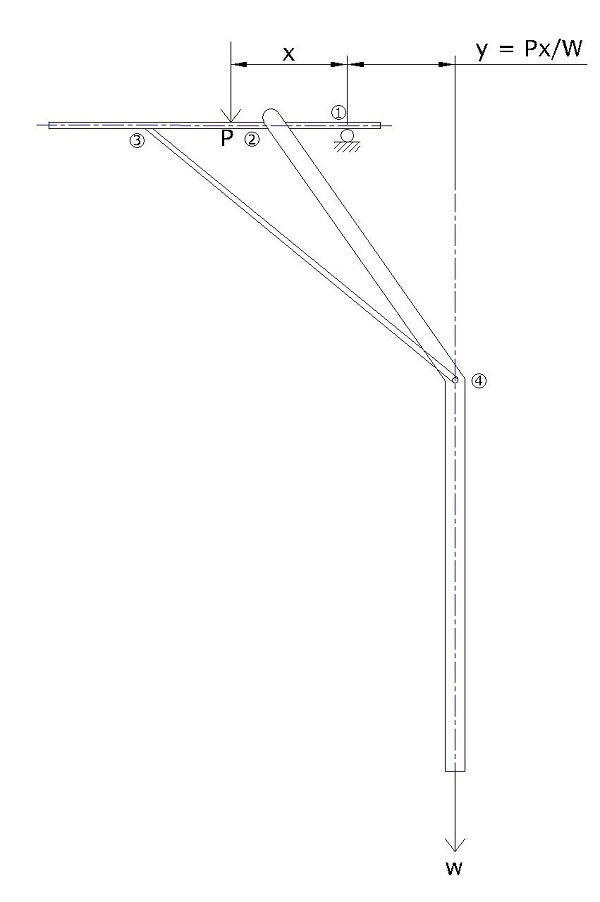
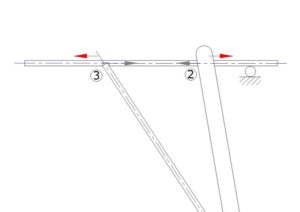
If all the joints were rigid enough to prevent all opening up, this is as good as following arrangement:
Post a Comment
You must be logged in to post a comment.









